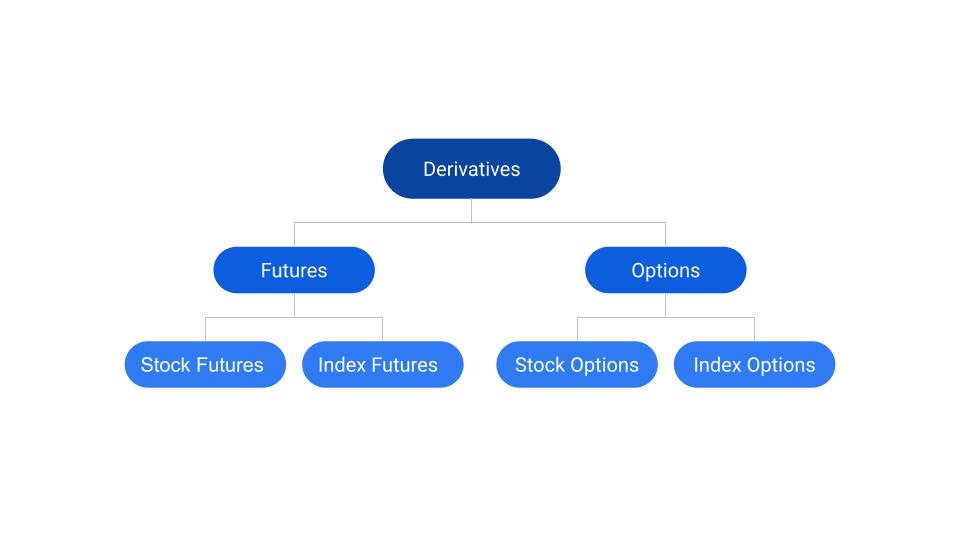
Futures and Options are types of derivatives. In order to understand Futures and Options, we will have to first understand what is a derivative. Derivative as the name suggests is derived from something. For instance, a stock or derivative is derived from Equities (stocks, shares whatever name you’re familiar with) similarly a commodity derivative is derived from commodities. Equities and Commodities both are assets. Below is an image that will help us in understanding the structure of derivatives for Equities.
The Futures in the Futures and Options
A future is a type of derivative which has an obligation on a future date. It is a type of contract in the futures and options segment. Let us look at an example of a Future for a better understanding. We have taken a stock of HDFC bank dated 18 July 2021 closed price of 1479.80 INR and Nifty Index with a close price of 15683.35 INR
Spot Price – The current market price of the underlying asset is known as the spot price. HDFC Bank Future’s price will depend on the current market price of HDFC Bank share or stock therefore, the price of HDFC bank’s share becomes the Spot price.
What are the limitations of Futures?
- It has a defined lot size like HDFC Bank has a lot size of 550 Shares.
- The lot size can vary from time to time, if the share price is increasing the lot size will decrease and if the share price is decreasing the lot size will increase. The lot size is inversely proportional to the spot price.
- The Future has an expiry on the last Thursday of the month.
- Expiry means that the spot price and the future’s price will both be the same on the last Thursday of the month.
- For example, HDFC BANK JUN FUT will expire on 24 June 2021 for July it will expire on 29 July 2021 meaning that we can only hold the July future till 29 July 2021 and so on for the month of August.
- Futures trades on a premium. The premiums depend on the market sentiments and therefore are indicative of the direction of the market.
Note – We can only trade in lots in the future. We can buy and sell the Future and hold it till the expiry. This makes derivatives a very unique financial instrument
As we can see in the above images that the share price of HDFC Bank is trading at 1479. Whereas one can also see that the Future price is trading at 1485 meaning that markets are positive. 1485-1479 = 6 points. The Futures are trading at a premium of 6 points, here 6×550 = 3300 INR indicating bullish sentiment. Similarly one can analyze the prices of the Index future as well.
What is an Option in the Futures and Options?
To understand an Option we must first have an understanding of the Futures. There are many components of an Option. The spot price we have already seen above. The strike price is something that makes an option very unique. Let us look at a sample image of BANKNIFTY.

There are two types of Options.
- Spot price – The current market price of the underlying asset.
- Strike price – The prices that are spread at regular intervals indicating the premiums
- Call Options – CE – When we assume that the markets will go up, we will buy CE
- Put Options – PE – When we assume that the markets will go down, we will buy PE
- Expiry – The date when the options will settle down to the value of zero (0)
- Premium – The amount that we will pay to book an option
The ‘E’ in the CE and PE represents European-style call and put options. There are again two cases here. Similarly, like Futures, we can buy and sell an individual option.
- When the underlying asset goes up or we can say the prices in an asset are in an uptrend we buy CE or sell PE.
- When the underlying asset goes down we buy or when the prices of an asset are in a downtrend we buy PE and sell CE.
Both buying a call and selling a put are the same phenomenon but with varying degrees of risk and returns for the investors. An uptrend means prices are on the rise continuously, and a downtrend is market prices are falling every day for a prolonged period of time for instance weeks or months. To know more about trends we can read market trends. The identification of trends is important to trade futures and options.